jewelrylpo.blogg.se - Gauss seidel algorithm python

Unfortunately this would require calculating $|A||x^i|$, which is not always possible. Since generally componentwise error bounds are much better, than normwise bounds, a stopping rule based on (2) would be better than (4). Below, we implement a standard Gauss-Seidel algorithm in Python: In 14: def. Then the tolerance $\epsilon$ is just the normwise backward error. Gauss-Seidel Iterations by the time it gets to the last equation it is. Since $\|A\|_\infty$ can be easily estimated. However, the manual computation of Gauss Seidel/Jacobi method can also be lengthy.Suppose that $A\mathbf$$ This method is fast and easy compared to the direct methods such as Gauss Jordan method, Gauss Elimination method, Cramer’s rule, etc. Compute the equilibrium probabilities of the Markov chain using Jacobi Iteration in Python.

Programs in any high level programming language can be written with the help of these Gauss-Seidel and Gauss Jacobi method algorithm and flowchart to solve linear simultaneous equations. I have the following function written for the Jacobi method and need to modify it to perform Gauss-Seidel function x,iter jacobi( A,b,tol,maxit ) jacobi iterations xzeros(size(b. determine under what conditions the Gauss-Seidel method always converges. Similarly to the Jacobi or Gauss-Seidel methods, the iteration starts with a guess (boldsymbol p0).Each method also requires a definition of the so-called search directions (boldsymbol dk) and the coefficients (alphak) defining the magnitude of the jumps along the search directions. recognize the advantages and pitfalls of the Gauss-Seidel method, and. solve a set of equations using the Gauss-Seidel method, (2). If absolute value of ((x – x0) / x) > er, then After reading this chapter, you should be able to: (1).

Declare the variables and read the order of the matrix n.

In Gauss Seidel method, the most recent values or fresher values are used in successive iterations. Guass-Seidel method is very similar to Gauss Jacobi method, and here are simple algorithm and flowchart for Gauss-Seidel and Gauss Jacobi method. For x ( 0) given, we build a sequence x ( k) such x ( k + 1) F ( x ( k)) with k N. For this, we use a sequence x ( k) which converges to the fixed point (solution) x. In this method, we should see that the variable absolute value coefficient is greater than or equal to sum of the absolute values of the coefficient of the remaining variables. The Gauss-Seidel method is an iterative method for solving linear systems such as. To get better values, the approximations in previous iterations are used. In Gauss Jacobi method, we assume x1, x2 and x3 as the three initial guesses. Whether it’s a program, algorithm, or flowchart, we start with a guess solution of the given system of linear simultaneous equations, and iterate the equations till the desired degree of accuracy is reached.

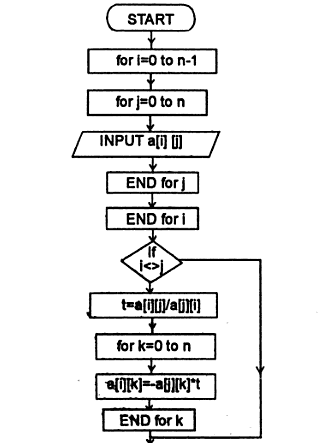
Both are based on fixed point iteration method. Gauss-Seidel and Gauss Jacobi method are iterative methods used to find the solution of a system of linear simultaneous equations.